定义:和牌型中,有东南西北4副刻(杠)子。
不算花牌的情况下,一共有136张牌。计算发牌上手直接天胡大四喜的概率
其中,东南西北全是刻的组合种类是$$\begin{equation}C^4_3C^4_3C^4_3C^4_3\tag{1}\end{equation}$$从其他的30种牌型里挑一种当将的种类是$$C^{30}_1C^4_2$$相乘即得到所有胡大四喜的组合。
全部组合则是$$C^{136}_{14}$$
概率为——
$$\frac{C^4_3C^4_3C^4_3C^4_3C^{30}_1C^4_2}{C^{136}_{14}} \approx 1e^{-12}\%=0.0000000000001\%$$
对应东南西北分别有1/2/3/4个杠组合是
$$C^4_1C^4_3C^4_3C^4_3 \tag{2.1}$$
$$C^4_2C^4_3C^4_3 \tag{2.2}$$
$$C^4_3C^4_3 \tag{2.3}$$
$$C^4_4 \tag{2.4}$$
概率是$$\frac{C^4_1C^4_3C^4_3C^4_3C^{30}_1C^4_2}{C^{136}_{15}}$$
$$\frac{C^4_2C^4_3C^4_3C^{30}_1C^4_2}{C^{136}_{16}}$$
$$\frac{C^4_3C^4_3C^{30}_1C^4_2}{C^{136}_{17}}$$
$$\frac{C^4_4C^{30}_1C^4_2}{C^{136}_{18}} $$
5个概率相加即是总概率。
下面讨论连续抓牌下,胡大四喜的概率,先不考虑其他人的策略和碰,假设所有牌都随机出现且可以被使用。
对于N张牌不出现杠的概率,需要12张凑成4个刻子,组合数量公式(1)计算相同为$$C^4_3C^4_3C^4_3C^4_3$$
在剩余的N-12牌里必须出现至少一个对子,因为3张也是允许的,且会出现2个对子或者更复杂情况,所以用互斥集合——$$总的组合数量-凑不成对子的组合数量$$
$$C^{136-16}_{N-12}-C^{30}_N(C^4_1)^N\tag{3}$$
其中当N>30时,根据抽屉原理必有一个对子。
得到公式,在打乱牌序中前N张牌,可以得到无杠大四喜的概率为
$$P_0 = \frac{C^4_3C^4_3C^4_3C^4_3(C^{136-16}_{N-12}-C^{30}_{N-12}(C^4_1)^{N-12})}{C^{136}_N}\tag{4.1}$$
对于有杠大四喜,四风的组合如式(2.1-2.4),将的组合如式(3),对应的概率为
$$P_1 = \frac{C^4_1C^4_3C^4_3C^4_3(C^{136-16}_{N-13}-C^{30}_{N-13}(C^4_1)^{N-13})}{C^{136}_N}\tag{4.2}$$
$$P_2 = \frac{C^4_2C^4_3C^4_3(C^{136-16}_{N-14}-C^{30}_{N-14}(C^4_1)^{N-14})}{C^{136}_N}\tag{4.3}$$
$$P_3 = \frac{C^4_3C^4_3(C^{136-16}_{N-15}-C^{30}_{N-15}(C^4_1)^{N-15})}{C^{136}_N}\tag{4.4}$$
$$P_4 = \frac{C^4_4(C^{136-16}_{N-16}-C^{30}_{N-16}(C^4_1)^{N-16})}{C^{136}_N}\tag{4.5}$$
当\(N\geq 18\)
$$P=\sum_{i=0}^4P_i$$
$$P=\frac{C^4_3C^4_3C^4_3C^4_3(C^{136-16}_{N-12}-C^{30}_{N-12}(C^4_1)^{N-12})+C^4_1C^4_3C^4_3C^4_3(C^{136-16}_{N-13}-C^{30}_{N-13}(C^4_1)^{N-13})+C^4_2C^4_3C^4_3(C^{136-16}_{N-14}-C^{30}_{N-14}(C^4_1)^{N-14})+C^4_3C^4_3(C^{136-16}_{N-15}-C^{30}_{N-15}(C^4_1)^{N-15})+C^4_4(C^{136-16}_{N-16}-C^{30}_{N-16}(C^4_1)^{N-16})}{C^{136}_N}$$
public static void combi(int n)
{
if(n<=18 || n>=136)
{
return;
}
//there're 5 situations for dasixi
// 1. each of 4 wind tile have 3 same tiles but not all 4
//denominator is 136 choose n
double denominator = Combinatorics.Combinations(136, n);
double numerator = 4*4*4*4;
numerator *= Combinatorics.Combinations(120,n-12) - Combinatorics.Combinations(30,n-12)*Math.Pow(4,n-12);
// 2. 1 of 4 wind, have 4 same tiles as a Gong, other 3 have 3 same tiles
double numerator1 = Combinatorics.Combinations(4,1) *4*4*4;
numerator1 *= Combinatorics.Combinations(120,n-13) - Combinatorics.Combinations(30,n-13)*Math.Pow(4,n-13);
numerator += numerator1;
// 3. 2 of 4 wind, have 4 same tiles as a Gong, other 2 have 3 same tiles
double numerator2 = Combinatorics.Combinations(4,2) *4*4;
numerator2 *= Combinatorics.Combinations(120,n-14) - Combinatorics.Combinations(30,n-14)*Math.Pow(4,n-14);
numerator += numerator2;
// 4. 3 of 4 wind, have 4 same tiles as a Gong, other 1 have 3 same tiles
double numerator3 = Combinatorics.Combinations(4,3) *4;
numerator3 *= Combinatorics.Combinations(120,n-15) - Combinatorics.Combinations(30,n-15)*Math.Pow(4,n-15);
numerator += numerator3;
// 5. 4 of 4 wind, have 4 same tiles as a Gong
double numerator4 = Combinatorics.Combinations(4,4);
numerator4 *= Combinatorics.Combinations(120,n-16) - Combinatorics.Combinations(30,n-16)*Math.Pow(4,n-16);
numerator += numerator4;
double result = numerator/denominator;
//console write result as percentage
Console.WriteLine(string.Format("{1} -- {0:P}", result,n));
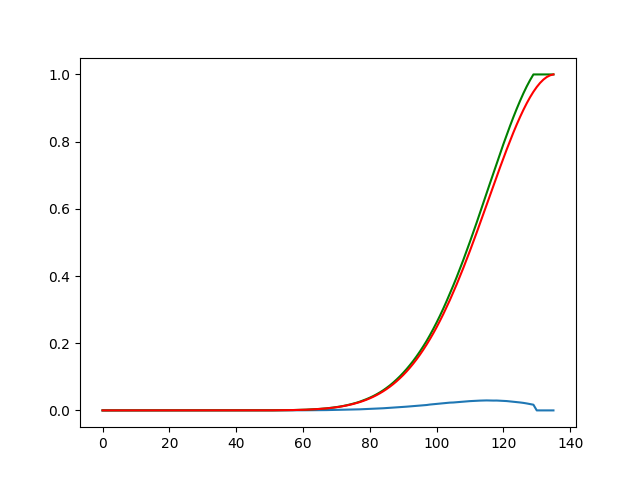
}概率曲线(红色)和随机运行100万次生成的曲线(绿色):